Нескінченність в математиці
Бескон е чностью в математиці. «Математичне нескінченне запозичене з дійсності, хоча і несвідомим чином, і тому воно може бути пояснено тільки з дійсності, а не з самого себе, не з математичної абстракції» (Енгельс Ф., Анти-Дюрінг, 1966, с. 396). Матеріальна основа математичного нескінченного може бути зрозуміла тільки за умови, що воно розглядається в діалектичній єдності з кінцевим. Кожна математична теорія пов'язана обов'язковим для неї вимогою внутрішньої формальної несуперечності. Тому виникає питання про те, як з'єднати цю вимогу з істотно суперечливим характером дійсності: Б. «Знищення цього протиріччя було б кінцем нескінченності» (там же, с. 47). Відповідь на це питання полягає в наступному. Коли в теорії меж розглядаються нескінченні межі lim an = ¥, або в теорії множин - нескінченні потужності, то це не призводить до внутрішніх формальних протиріч у вказаних теоріях лише тому, що ці різні спеціальні види математичних Б. є лише вкрай спрощеними, схематизованих образами різних сторін Б. дійсного світу.
Завдання цієї статті обмежуються вказівкою на різні підходи до Б. в математиці, освітлювані детальніше в інших статтях.
1) Уявлення про нескінченно малих і нескінченно великих змінні величини є одним з основних в математичному аналізі. Передувала сучасному підходу до поняття нескінченно малої концепція, за якою кінцеві величини складалися з нескінченно великого числа нескінченно малих «неподільних» (див. «Неделімих» метод ), Трактуючи не як змінні, а як постійні і менші будь-якої кінцевої величини, може служити одним з прикладів незаконного відриву безконечного від кінцевого: реальний сенс має тільки розкладання кінцевих величин на необмежено зростаюче число необмежено відбувають доданків.
2) Зовсім в іншій логічній обстановці Б. з'являється в математиці у вигляді «невласних» нескінченно видалених геометричних образів (див. Нескінченно видалені елементи ). Тут, наприклад, нескінченно видалена точка на прямій а розглядається як особливий постійний об'єкт, «приєднаний» до звичайних кінцевих точок. Однак нерозривний зв'язок нескінченного з кінцевим виявляється і тут, хоча б при проектуванні з центру, що лежить поза прямою, при якому нескінченно віддаленої точки виявляється відповідної пряма, що проходить через центр проектування і паралельна основною прямою а.
Аналогічний характер має поповнення системи дійсних чисел двома «невласними» числами + ¥ і - ¥, відповідне багатьом запитам аналізу і теорії функцій дійсного змінного. Можна підійти з такою ж точки зору і до поповнення ряду натуральних чисел 1, 2, 3, ..., трансфинитное числами w, w + 1, ..., 2 w, 2 w + 1, .... У зв'язку з відмінністю між змінними нескінченно малими і нескінченно великими величинами, з одного боку, і «невласними» нескінченно великими числами, які розглядаються як постійні , - з іншого, виникли терміни «потенційна» Б. (для перших) і «актуальна» Б. (для других). У цьому первісному розумінні (про інше, сучасному розумінні, див. Нижче) спір між прихильниками актуальною і потенційної Б. можна вважати закінченим. Нескінченно малі і нескінченно великі, що лежать в основі визначення похідної (як стосунки нескінченно малих) і інтеграла (як суми нескінченно великого числа нескінченно малих) і прилеглих сюди концепцій математичного аналізу, повинні сприйматися як «потенційні». Поряд з цим в належній логічній обстановці в математику цілком закономірно входять і «актуальні» нескінченно великі «невласні» числа (і навіть у багатьох різних аспектах: як кількісні і порядкові трансфінітні числа в теорії множин, як невласні елементи + ¥ і - ¥ системи дійсних чисел і т.д.).
В математиці доводиться мати справу з двома способами приєднання до числової системи безконечних «невласних» елементів.
а) З проектної точки зору на прямій знаходиться одна «нескінченно видалена точка». У звичайній метричній системі координат цій точці природно приписати абсциссу ¥. Таке ж приєднання до числової системи однієї Б. без знаку вживається в теорії функцій комплексного змінного. В елементарному аналізі при вивченні раціональних функцій
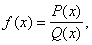
де Р (х) і Q (x) - многочлени, в тих точках, де Q (x) має нуль вищого порядку, ніж Р (х), природно покласти f (x) = ¥. Для невласного елементу ¥ встановлюються такі правила дій:
¥ + а = ¥, якщо а звичайно;
¥ + ¥ не має сенсу;
¥ · а = ¥, якщо а ¹ 0;
¥ · 0 не має сенсу.
Нерівності за участю ¥ не розглядаються: безглуздо питати, більше або менше ¥, ніж кінцеве а.
б) При вивченні дійсних функцій дійсного змінного систему дійсних чисел доповнюють двома невласними елементами + ¥ і - ¥. Тоді можна покласти, що - ¥ <а <+ ¥ для будь-якого кінцевого а, і зберегти основні властивості нерівностей в розширеній числовій системі. Для + ¥ і - ¥ встановлюються такі правила дій:
(+ ¥) + а = + ¥, якщо а ¹ - ¥;
(- ¥) + а = - ¥, якщо а ¹ + ¥;
(+ ¥) + (- ¥) позбавлене сенсу;
(+ ¥) '· а = + ¥, якщо а> 0;
(+ ¥) 'а = - ¥, якщо а <0;
(- ¥) '· а = - ¥, якщо a> 0;
(- ¥) 'а = + ¥, якщо а <0;
(+ ¥) '0 і (¥)' 0 позбавлені сенсу.
У кожному математичному міркуванні слід віддавати собі звіт, користуємося ми в ньому справжньою (не розширення) числовий системою або розширеною, і в якому саме з двох вказаних сенсів.
3) Основний інтерес, а й основні труднощі математичного учення о Б. зосереджуються зараз на питанні про природу безконечної безлічі математичних об'єктів. Слід, зокрема, мати на увазі, що досягнута нині повна виразність і закінченість теорії нескінченно великих і нескінченно малих змінних величин полягає лише в зведенні всіх труднощів цієї теорії до питання обгрунтування вчення про число, в яке істотно входить представлення про Б. системи чисел. Твердження про те, що у нескінченно мало, має сенс тільки при вказівці характеру зміни у залежно від будь-якого іншого змінного х; наприклад, говорять, що у нескінченно мало при х ® а, якщо при будь-якому e> 0 існує таке d> 0, що з | х - a | <D випливає | у | <E. У самий це визначення вже входить припущення, що функція y = f (x) визначена для нескінченної кількості значень х (наприклад, для всіх дійсних х, досить близьких до а). Про нескінченних множинах в математиці докладніше див. множин теорія .
В теорії множин термінам «актуальна» і «потенційна» Б. додають зазвичай глибокий сенс, який не має нічого спільного з найменуванням кожної безконечної потужності «актуально нескінченним числом». Справа в тому, що нескінченні системи математичних об'єктів (наприклад, натуральних або дійсних чисел) ніколи не задаються простим перерахуванням, як це можливо для кінцевих систем об'єктів. Було б очевидним абсурдом припускати, що будь-хто «утворив» безліч натуральних чисел, перерахувавши їх фактично «все» одне за іншим. Насправді безліч натуральних чисел вивчають, виходячи з процесу утворення його елементів переходом від n до n + 1. У разі континууму дійсних чисел вже розгляд одного його елементу - дійсного числа - призводить до вивчення процесу утворення його послідовних наближених значень, а розгляд всієї безлічі дійсних чисел приводить до вивчення загальних властивостей такого роду процесів утворення його елементів. У цьому саме сенсі сама Б. натурального ряду, або системи всіх дійсних чисел (континуум), може характеризуватися як Б. лише «потенційна». Точці зору потенційної Б. протиставляється погляд на безконечну безліч як «актуально» задані, незалежно від процесу їх освіти. З'ясування питання про те, якою мірою і за яких умов при вивченні безконечної безлічі законне таке абстрагування від процесу їх освіти, ще не можна вважати закінченим. Див. множин теорія , логіка , Математика .
А. Н. Колмогоров.