групова швидкість

ГРУПОВА ШВИДКІСТЬ хвиль - швидкість руху групи або цуга хвиль, що утворюють в кожен даний момент часу локалізований в просторі хвильової пакет , Огинає догрого є плавну в масштабі довжини хвилі 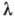криву (рис. 1) (див. Хвилі). У лінійних середовищах, де дотримується суперпозиції принцип , Його можна розглядати як набір гармонич. хвиль з частотами в інтервалі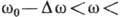 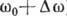), Тим більше вузькому, ніж плавніше і протяжні огинає групи. довжина пакета 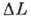і ширина його спектру 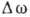обмежені знизу співвідношенням 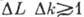, де хвильове число k пов'язано з частотою 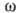дисперсійним співвідношенням .

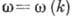Якщо середовище не володіє дисперсією, то все гармонич. хвилі поширюються з однієї і тієї ж фазовою швидкістю, і пакет поводиться як строго стаціонарна хвиля - його Г. с. співпадає з фазової швидкістю 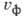. При наявності дисперсії хвилі разл. частот поширюються з різними швидкостями і форма обвідної спотворюється. Однак для сигналів з досить вузьким спектром, коли фазові швидкості гармонич. хвиль, що утворюють хвильовий пакет, мало відрізняються один від одного, і на не дуже великих відстанях, коли форма обвідної приблизно зберігається, вплив дисперсії позначається лише на швидкості переміщення обвідної, к-раю і є Г. с. Оскільки поширення двох синусоїдальних хвиль з близькими частотами 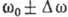пакету описується виразами

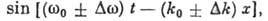
то швидкість їх обвідної дорівнює 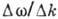, Що в межі призводить до ф-ле 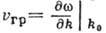. На рис. 2 представлені три послідовних миттєвих знімка сигналу з вузьким спектром, що поширюється в середовищі з дисперсією. Нахил пунктирних прямих, що з'єднують точки однакової фази (напр., Максимуми), характеризує фазову швидкість; нахил прямих, що з'єднують відповідні точки обвідної (початку і кінця сигналу), характеризує Р. с. сигналу. Якщо при поширенні сигналу максимуми і мінімуми рухаються швидше, ніж огинає, то це означає, що фазова швидкість даної групи хвиль перевищує її Р. с. (Рис. 2, а). При поширенні сигналу в його "хвостовій" частини виникають все нові максимуми, к-які поступово переміщаються вперед, досягають його головної частини і там зникають. Такий стан має місце у випадку т. Н. нормальної дисперсії, т. е. в середовищах, де показник заломлення 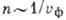збільшується зі зростанням частоти гармонич. хвилі 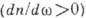. Таку дисперсію зв. також негативною, оскільки з ростом k фазова швидкість хвилі убуває. Приклади середовищ з нормальною дисперсією - речовини, прозорі для оптич. хвиль, хвилеводи, ізотропна плазма та ін. Однак в ряді випадків спостерігається аномальна (позитивна) дисперсія середовища 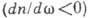; в цих випадках Р. с. сигналу перевищує його фазову швидкість 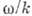. Максимуми і мінімуми з'являються в передній частині сигналу (рис. 2, б), переміщаються назад і зникають в його хвості. Аномальна дисперсія характерна для капілярних хвиль на поверхні води (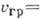 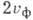), Для ел - магн. і акустич. хвиль в середовищах з резонансним поглинанням, а також при потужність. умовах - для хвиль в периодич. структурах (кристали, що уповільнюють системи і т. п.). При цьому можлива навіть ситуація, при якій Г. с. спрямована протилежно фазової. Хвилі, що володіють цією властивістю, наз. зворотними.

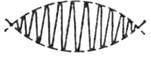
Мал. 1. Хвильовий пакет.

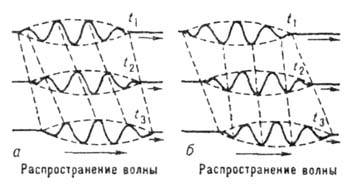
Мал. 2. Послідовні моментальні знімки групи хвиль в моменти часу t1, t2, t 3 в разі нормальної дисперсії (A) і в разі аномальної дисперсії (б).

Г. с. визначає швидкість і напрямок перенесення енергії хвилями. В анізотропних середовищах (напр., Кристалах, плазмі в пост. Магн. Поле), де показники заломлення хвиль залежать від частоти і напрямку поширення, Г. с. визначається як векторна похідна 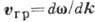і зазвичай не збігається за напрямком з фазової швидкістю. У середовищах з сильним поглинанням замість Г. с. 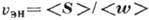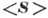вводять величину, що характеризує швидкість перенесення енергії , де - пор. щільність потоку енергії, а 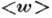- пор. щільність енергії в хвилях. У прозорих середовищах величини 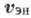і 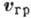збігаються.

Поняття Р. с. відіграє важливу роль і в фізики , І в техніці, оскільки всі методи вимірювання швидкостей поширення хвиль, пов'язані з запізненням сигналів (в т. Ч. швидкості світла ), Дають Г. с. Вона фігурує при вимірюванні дальності в гідро- і радіолокації , При зондуванні іоносфери, в системах управління космічних. об'єктами і т. д. Відповідно до відносності теорії Г. с. не може цревишать швидкості поширення світла у вакуумі, т. е. завжди .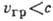

Літ .: Горелік Р. С., коливання і хвилі, 2 изд., M., 1959; Гінзбург В. Л., Поширення електромагнітних хвиль в плазмі, 2 изд., M., 1967, Крауфорд Ф., Колн, пров. з англ., 3 вид., M., 1984; Пірс Д ж., Майже все про хвилях, пров. з англ., M., 1976.

M. А. Міллер, E. В. Суворов.

покажчик >>