Реферат з математики на тему "Велика теорема Ферма"

«Велика теорема Ферма»

2016

Велика теорема Ферма

Видання 1670 року «Арифметики» Діофанта включає коментар Ферма, зокрема його «останню теорему» (Observatio Domini Petri de Fermat)

Велика теорема Ферма (або Остання теорема Ферма) - одна з найпопулярніших теорем математики. Її умова формулюється просто, на «шкільному» арифметичному рівні, однак доказ теореми шукали багато математики більше трьохсот років. доведено в 1994 році Ендрю Уайлсом .

Теорема стверджує, що:

для будь-якого натурального числа 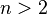рівняння

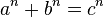
не має рішень в цілих ненульових числах .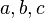

Зустрічається більш вузький варіант формулювання, який стверджує, що це рівняння не має натуральних рішень. Однак очевидно, що якщо існує рішення для цілих чисел, то існує і рішення в натуральних числах. Справді, нехай 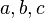- цілі числа, що дають рішення рівняння Ферма. якщо 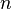парно, то 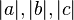теж будуть рішенням, а якщо непарній, то перенесемо всі ступені негативних значень в іншу частину рівняння, змінивши знак. Наприклад, якби існувало рішення рівняння 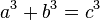і при цьому 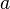негативно, а інші позитивні, то 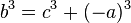, І отримуємо натуральні рішення 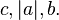Тому обидві формулювання еквівалентні.

Узагальненнями затвердження теореми Ферма є спростована гіпотеза Ейлера і відкрита гіпотеза Ландера - Паркина - Селфрідж .

Історія

для випадку 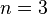цю теорему в X столітті намагався довести ал-Ходжанді , Але його доказ не збереглося.

У загальному вигляді теорема була сформульована П'єром Ферма в 1637 році на полях «Арифметики» Діофанта . Справа в тому, що Ферма робив свої позначки на полях читаються математичних трактатів і там же формулював прийшли на розум завдання і теореми. Теорему, про яку ведеться мова, він записав з припискою, що знайдене ним дотепне доведення цієї теореми надто довге, щоб його можна було помістити на полях книги:

«Навпаки, неможливо розкласти куб на два куба, біквадрат на два біквадрата і взагалі ніяку ступінь, велику квадрата, на два ступені з тим же показником. Я знайшов цьому воістину чудесний доказ, але поля книги занадто вузькі для нього ».

Доказ самого Ферма для випадку 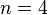в сорок п'ятому коментарі до «Арифметиці» Діофанта

Ферма призводить тільки доказ, як рішення задачі, зводиться до четвертого ступеня теореми 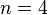, В сорок п'ятому коментарі до «Арифметиці» Діофанта і в листі до Каркаві (серпень 1659 року). Крім цього, Ферма включив третю ступінь теореми 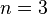в список завдань, що вирішуються методом нескінченного спуску .

Ейлер в 1770 році довів теорему для випадку 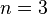, Діріхле і Лежандр в 1 825 - для 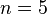, Ламі - для 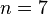. Куммер показав, що теорема вірна для всіх простих n, менших 100, за можливим винятком т. н. іррегулярних простих 37, 59, 67.

Над повним доказом Великої теореми працювало чимало видатних математиків і безліч дилетантів-аматорів; вважається, що теорема стоїть на першому місці за кількістю некоректних «доказів». Проте, ці зусилля призвели до отримання багатьох важливих результатів сучасної теорії чисел . Давид Гільберт в своїй доповіді «Математичні проблеми» на II Міжнародному конгресі математиків ( 1900 ) Так відгукнувся про цю проблему:

Проблема докази цієї нерозв'язності являє разючий приклад того, яке спонукає вплив на науку може надати спеціальна і на перший погляд незначна проблема. Бо, побуждённий завданням Ферма, Куммер прийшов до введення ідеальних чисел і до відкриття теореми про однозначне розкладанні чисел в кругових полях на ідеальні прості множники - теореми, яка тепер, завдяки узагальнень на будь-яку алгебраїчну числову область, отриманим Дедекіндом і Кронекером , Є центральною в сучасній теорії чисел і значення якої виходить далеко за межі теорії чисел в область алгебри і теорії функцій.

В 1908 році німецький любитель математики Вольфскель заповідав 100 000 німецьких марок тому, хто доведе теорему Ферма. Однак після війни премія знецінилася .

У 1980-х роках з'явився новий підхід до вирішення проблеми. з гіпотези Морделла , доведеною Герд Фалтінгс в 1983 році , Випливає, що рівняння 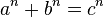при 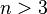може мати лише кінцеве число взаємно простих рішень.

Останній, але найважливіший, крок в доведенні теореми був зроблений Уайлсом у вересні 1994 року . Його 130-сторінковий доказ було опубліковано в журналі « Annals of Mathematics ». Доказ засноване на припущенні німецького математика Герхарда Фрая про те, що Велика теорема Ферма є наслідком гіпотези Таніями - Сімура (Це припущення було доведено Кеном Рібет за участю Ж.П. Серра ).

Перший варіант свого докази Уайлс опублікував в 1993 році (Після 7 років напруженої роботи), але в ньому незабаром був виявлений серйозний пробіл, який за допомогою Річарда Лоуренса Тейлора вдалося досить швидко усунути. В 1995 році був опублікований завершальний варіант.

Колін Мак-Ларт зазначив, що доказ Уайлса може бути спрощено, щоб не припускати існування так званих «великих кардиналів».

«Ферматістов»

Авторське свідоцтво, видане Міністерством освіти і науки України на доказ теореми Ферма Г. А. Середкин і Л. В. Шаповалової

Простота формулювання теореми Ферма (доступна в розумінні навіть школяреві), а також складність єдиного відомого докази (або незнання про його існування), надихають багатьох на спроби знайти інше, більш просте, доказ. Людей, які намагаються довести теорему Ферма елементарними методами, називають «ферматістов» або «ферматікамі». Ферматістов часто не володіють основами математичної культури і допускають помилки в арифметичні дії або логічних, хоча деякі представляють досить витончені «докази», в яких важко знайти помилку.

Доводити теорему Ферма в середовищі любителів математики було настільки популярно, що в 1972 році журнал «Квант» , Публікуючи статтю про теорему Ферма, супроводжував її наступною припискою:

Редакція «Кванта» зі свого боку вважає за необхідне повідомити читачів, що листи з проектами доказів теореми Ферма розглядатися (і повертатися) не будуть.

німецькому математику Едмунда Ландау дуже докучали «ферматістов». Щоб не відволікатися від основної роботи, він замовив кілька сот бланків з наступним текстом:

Шановний ...! Дякую Вам за надіслану Вами рукопис з доказом Великої теореми Ферма. Перша помилка перебуває на сторінці ... в рядку ...

Знаходити помилку і заповнювати прогалини в бланку він доручав своїм аспірантам.

Примітно, що окремі ферматістов домагаються публікації своїх (невірних) «доказів» в ненауковою пресі, яка роздмухує їх значення до наукової сенсації . Втім, іноді такі публікації з'являються і в поважних наукових виданнях, як правило, з подальшими спростуваннями. Серед інших прикладів:

• Брошура В. І. Будкина, видана в Ярославлі під назвою «Методика пізнання" істини ". Доказ Великої теореми Ферма »(47 с., 5000 прим., Верхньо-Волзьке книжкове видавництво, 1975 ).

• Книга Л. Ш. Райхеля «Велика теорема», видана в Ленінграді в 1990 році.

• Свідоцтво про реєстрацію авторських прав на твір «доказ теореми Ферма», видане Міністерством освіти і науки України Л. В. Шаповалової та Г. А. Середкин. Слід пояснити, що цей документ не засвідчує будь-яким чином правильність докази, а лише реєструє авторські права на поданий до Міністерства освіти і науки друкована праця; на це міністерство покладено обов'язок ведення реєстру таких свідчень.

Теорема Ферма в культурі і мистецтві

Велика теорема Ферма стала символом запеклій наукової проблеми і в цій якості часто згадується в белетристиці. Далі перераховані деякі твори, в яких теорема не просто згадана, але є істотною частиною сюжету або ідеології твори.

• У повісті Е. Велтистова «Переможець неможливого» один Сироїжкіна і Електроніка Вова Корольков в якості вільного завдання з математики довів Велику теорему Ферма.

• У телесеріалі « Зоряний шлях »Капітан космічного корабля Жан-Люк Пікар був спантеличений розгадкою Великої теореми Ферма в другій половині XXIV століття . Таким чином, творці фільму припускали, що рішення у Великої теореми Ферма не буде в найближчі 400 років. серія « рояль »З цим епізодом була знята в 1989 році , коли Ендрю Уайлс був на самому початку своїх робіт. Насправді рішення було знайдено всього через 5 років.

• В оповіданні Артура Порджес «Саймон Флегг і диявол» професор Саймон Флегг звертається за доведенням теореми до диявола. За цим оповіданням знятий ігровий науково-популярний фільм « Математик і чорт »(СРСР, тисячі дев'ятсот сімдесят дві , Виробництво Центрнаучфільм, творче об'єднання «Райдуга», режисер Райтбурт ).

• В оповіданні Кіра Буличова «Мрія заочника» студент-заочник Гаврилов приходить до професора Мінца і приносить куплену курсову роботу, в якій наводиться доказ теореми, з проханням пояснити, що він написав.

• У присвяченій Хеллоуїну 1995 року серії « Сімпсонів »Двовимірний Гомер Сімпсон випадково потрапляє в третій вимір. Під час його подорожі в цьому дивному світі в повітрі ширяють геометричні тіла і математичні формули, включаючи рівність 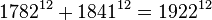. Калькулятор з точністю не більше 9 значущих цифр підтверджує це рівність:

1782 12 + 1841 12 = 2541210258614589176288669958142428526657 ≈ 254 121 026 х 10 31,

Одна тисяча дев'ятсот двадцять два 12 = 2541210259314801410819278649643651567616 ≈ 254 121 026 х 10 31.

Проте, навіть без обчислення точних значень легко бачити, що рівність невірно: ліва частина - непарне число , А права частина - парне.

• У першому виданні « мистецтва програмування » Дональда Кнута теорема Ферма наведена в якості вправи з математичним ухилом на самому початку книги і оцінена максимальним числом (50) балів, як «дослідницька проблема, яка (наскільки це було відомо автору в момент написання) ще не отримала задовільного рішення. Якщо читач знайде рішення цього завдання, його вимагають опублікувати його; крім того, автор даної книги буде дуже вдячний, якщо йому повідомлять рішення якомога швидше (за умови, що воно правильно) ». У третьому виданні книги цю вправу вже вимагає знань вищої математики і оцінюється лише в 45 балів.

• У книзі Стіга Ларссона « Дівчина, яка грала з вогнем »Головна героїня Лісбет Саландер, що володіє рідкісними здібностями до аналітики і фотографічною пам'яттю, як хобі зайнята доказом Великої теореми Ферма, на яку вона натрапила, читаючи фундаментальну працю« Вимірювання в математиці », в якому наводиться і доказ Ендрю Уайлса. Лісбет не хоче вивчати готове доказ, а головним інтересом стає пошук власного рішення. Тому весь свій вільний час вона присвячує самостійного пошуку «чудового докази» теореми великого француза, але раз по раз заходить в глухий кут. В кінці книги Лісбет знаходить підтвердження, яке не тільки абсолютно відмінно від запропонованого Уайлсом, але і є настільки простим, що сам Ферма міг би його знайти. Однак, після поранення в голову вона його забуває, і Ларссон не приводить ніяких подробиць цього докази.

• Мюзикл «Останнє танго Ферма», виданий інститутом Клея , Створений в 2000 році Дж. Розенблума і Дж. С. Лессер за мотивами реальної історії Ендрю Уайлса. Головний герой на ім'я Деніел Кін завершує доведення теореми, а дух самого Ферма намагається йому перешкодити.

• За кілька днів до своєї смерті Артур Кларк встиг відрецензувати рукопис роману « Остання Теорема », Над якою він працював у співавторстві з Фредеріком. Книга вийшла вже після смерті Кларка.

• В оповіданні Наталії Дарьяловой «Велика і загадкова» сюжет будується на теоремі Ферма. Розповідається про те, як молода людина, будучи студентом, зайнявся теоремою Ферма, згодом став математиком, отримав кілька важливих наукових результатів, але абсолютно занапастив своє особисте життя.

• У романі П. А. Загребельного «Розгін» скромний викладач математики з Одеси зумів довести теорему, через деякий час став академіком і очолив дуже серйозне київське НВО , Що займається створенням електронно-обчислювальних систем .

• А. П. Казанцев в романі «Найгостріше шпаги» в 1983 році запропонував оригінальну версію відсутності докази самого П'єра Ферма.

література

Російською

Англійською

• Donald C. Benson. The Moment of Proof: Mathematical Epophanies. - Oxford University Press, 1999. - ISBN 0-19-513919-4 .

• Faltings, Gerd (1995). The Proof of Fermat's last theorem by R. Taylor and A. Wiles , Notices of the AMS (42) (7), 743-746.

• Daney, Charles (2003). The Mathematics of Fermat's last theorem . Retrieved Aug. 5, 2004.

• O'Connor, JJ & and Robertson, EF (1996). Fermat's last theorem. The history of the problem . Retrieved Aug. 5, 2004.

• Shay, David (2003). Fermat's last theorem. The story, the history and the mystery . Retrieved Aug. 5, 2004.