Книга: Статистика: навчальний посібник

Глава 1

ДОЦІЛЬНІСТЬ І ПОСЛІДОВНІСТЬ ЗАСТОСУВАННЯ СТАТИСТИЧНИХ МЕТОДІВ ПРИ АНАЛІЗІ СТАТИЧНИХ ПРОЦЕСІВ І ЯВИЩ

1.1. Методи дослідження однорідності досліджуваного об'єкта і типологічна угруповання

Однією з відмінних рис бурхливого розвитку науки є широке застосування статистичних методів і обчислювальної техніки в освоєнні інформації. В даний час неможливо уявити собі дисципліну, яка не користувалася б в процесі пізнання методами чисельного вираження закономірностей, зв'язків, залежності, вимірювання тенденції і т. Д. Це, зокрема, відноситься і до економічних наук.

У статистичній літературі велика увага приділяється вивченню і застосуванню окремих статистичних методів і прийомів, але зовсім недостатньо висвітлені питання доцільності і послідовності використання того чи іншого статистичного методу, їх комплексного застосування, поєднання різних методів. Абсолютизація того чи іншого методу дослідження нічого, крім шкоди, не приносить. Тільки поєднання різних методів може дати помітний ефект. Саме з цих позицій і потрібно оцінювати роль і місце статистичного моделювання в системі пізнання різних процесів і явищ. У даній роботі зроблена спроба систематизувати методику комплексного застосування статистичних методів в економічних дослідженнях, розглянуто доцільність та послідовність використання статичних методів і прийомів при аналізі статичних і динамічних процесів.

Першим етапом дослідження є накопичення (збір) необхідних відомостей про досліджуваному об'єкті. Якщо спостережень не дуже багато, то можна провести впорядкування, розташувавши їх в порядку зростання або зменшення, т. Е. Побудувати ранжирування ряди. Якщо ж спостережень багато, то доводиться вдаватися до їх угрупованню. Статистичні ряди носять найрізноманітніший характер, мають різне призначення і в різних цілях можуть використовуватися в економічному аналізі. Одні статистичні ряди є варіаційними рядами розподілу. Ці ряди показують розподіл одиниць досліджуваної сукупності за окремими групами, виділеним по будь-якою ознакою. Іншим різновидом статистичних рядів є послідовність чисел, що відбивають величину того чи іншого показника в часі. Це так звані ряди динаміки. Вони дозволяють аналізувати зміну будь-яких явищ в часі, про це йтиметься нижче. Не применшуючи значення часових рядів, слід зазначити, що варіаційним рядах розподілу в статистичному аналізі належить особливе місце, бо тільки за допомогою розподілу складних сукупностей на якісно однорідні групи можна вивчати їх структуру, співвідношення між частинами цілого і т. П., Без чого немислимий ніякий економічний аналіз. Ряди розподілу можуть будуватися за якісними (атрибутивною) і за кількісними ознаками, за однією ознакою і за кількома, надаючи тим самим широкі можливості дослідникам при вивченні складних економічних явищ. Ряди розподілу можуть бути представлені або в табличній формі, або в геометричній, т. Е. Графічної. Статистична сукупність, представлена ​​у вигляді рангового ряду розподілу, графічно зображується у вигляді огіви. Вона будується так: на осі абсцис наносяться номера елементів сукупності по ранжиру, а на осі ординат відкладаються значення ознаки. Огіва наочно показує інтенсивність зміни досліджуваного ознаки. Варіаційні ряди розподілу зображаються графічно у вигляді полігонів і гістограм. У вигляді полігонів зазвичай зображуються дискретні варіаційні ряди розподілу. При цьому значення ознаки відкладають на осі абсцис, а частоти (або частості) - на осі ординат. Вершини ординат з'єднують прямими лініями, в результаті чого отримують полігон (багатокутник). У вигляді полігону можна уявити і інтервальні варіаційні ряди. Для цього за окремі значення ознаки приймаються середні значення інтервалів. Інтервальні ж варіаційні ряди найчастіше зображують у вигляді гістограми, в якій частоти висловлюють у вигляді прямокутників відповідної довжини, а підстави прямокутників, які спираються на вісь абсцис, відповідають інтервалу значення ознаки (рис. 1).

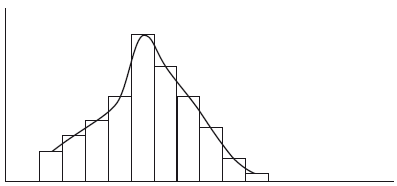
Мал. 1. Гістограма і полігон розподілу

Розрізняють одновершинні і многовершинная розподілу. Многовершінной розподілу, як правило, є ознакою неоднорідності досліджуваної сукупності. З різноманітності форм одновершинная кривих розподілів можна виділити наступні найбільш характерні типи: симетричні, помірно асиметричні, вкрай асиметричні.

У практиці зазвичай рідко зустрічаються ідеально симетричні розподілу, частіше помірно асиметричні, в яких частоти з одного боку від центру розсіювання зменшуються помітно швидше, ніж з іншого. Асиметричний розподіл в межі стає вкрай асиметричним - в цьому випадку найбільша частота розташована на одному з кінців розподілу.

При вирішенні деяких питань зручніше користуватися накопиченими частотами розподілу. Крива накопичених частот розподілу носить назву «кумулята розподілу». При побудові кумуляти на осі абсцис відкладаються значення ознаки, на осі ординат - накопичені частоти. Побудова варіаційного ряду розподілу та його графічне зображення дозволяють отримати перше уявлення про його найбільш характерних загальних рисах. У той же час статистичне вивчення сукупності не може обмежитися лише простим упорядкуванням спостережуваних величин. До того ж ряди розподілу та їх графіки бувають досить громіздкими, тому що включають в себе всю вихідну інформацію. Тому найбільш раціональним шляхом статистичного опису розподілу буде обчислення певних числових характеристик, що відображають реальні властивості сукупності. До таких характеристик насамперед належать характеристики центральної тенденції ряду розподілу, т. Е. Знаходження його центрального значення; розсіювання значень ознаки щодо центру розподілу; асиметрії та гостровершинності розподілу. Вивчення статистичних характеристик розподілів доцільно почати з розгляду найбільш простих і в той же час найчастіше використовуваних в статистичному аналізі, т. Е. З вивчення середніх величин; потім навчитися вимірювати варіацію, вивчити заходи скошеності і гостровершинності. Всі ці показники тих чи інших особливостей розподілу становлять єдину систему статистичних показників.

Однак застосування тих чи інших статистичних методів передбачає перш за все однорідність досліджуваної сукупності: не можна, наприклад, аналізувати сукупність, що складається з різних категорій господарств, що включає підприємства різної спеціалізації і т. Д. Для успішного вирішення завдань необхідно глибоке розуміння суті досліджуваного процесу або явища. З огляду на складність, неоднорідність економічних явищ і процесів, необхідно проводити аналіз таким чином, щоб найбільш істотні відмінності між окремими групами явищ не затушовувалися, а виділялися для більш успішного їх вивчення. У той же час об'єднання в групи схожих однотипних явищ допомагає виявити їх риси та особливості, які при вивченні кожного явища