натуральне числення

Натур а льно исчисл е ня, обчислення природного виведення, натуральна дедукція, загальна назва логічних числень, введених і вивчених в 1934 німецьким логіком Г. Генценом (і незалежно польським логіком С. Яськовського) з метою формалізації процесу логічного висновку, як можна більш точно відтворює структуру звичайних змістовних міркувань, а також для вирішення ряду важливих завдань метаматематики (В тому числі для доказу несуперечності арифметики натуральних чисел). Основним об'єктом Н. і. можна вважати відношення (формальної) виводимості, що позначається символом , Що володіє, за визначенням, властивістю А 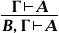(Дозвіл посилити посилки), 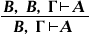(Дозвіл опускати одну із співпадаючих посилок), 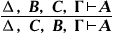(Дозвіл переставляти посилки). У різних формулюваннях Н. і. вид і кількість структурних правил різні; наприклад, розуміючи під Д і Г не послідовно, а просто кінцеві безлічі (невпорядковані) формул, можна обійтися без правил перестановки посилок; звичайна угода, що кожен елемент входить в нього лише один раз, робить непотрібним правило скорочення повторюваних посилок, і т.п. Крім того, в Н. і. входять логічні правила виводу, що регламентують процедуру введення і видалення (усунення, виключення) символів логічних операцій і описують (як і аксіоми «звичайних» логічних числень; див., наприклад, логіка висловлювань ) Властивості цих операцій. Ось правила класичного Н. і. висловлювань:

Вступ

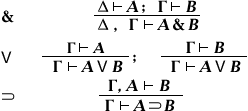
(Так звана «теорема про дедукції», див. дедукція )

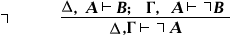
(Reductio ad absurdum, або приведення до безглуздості, см. Доказ від противного ) Видалення

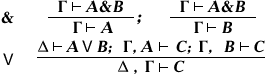
(Так званий доказ розбором випадків)

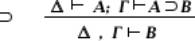
(Modus ponens, або схема висновку)

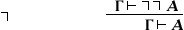
(Так званий закон зняття подвійного заперечення). (В дужках вказана інтерпретація деяких правил в термінах традиційної логіки; інтерпретація інших правил - та ж, що у відповідних аксіом звичайного числення висловів, перефразування яких вони є.) Додавання до цього списку відповідних правил введення і видалення для кванторів призводить до Н. і. предикатів. заміна правила 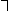-Віддалене на так зване правило слабкого 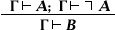( «З протиріччя слід будь-яке висловлювання», див. протиріччя принцип ) Призводить до інтуїционістському (конструктивному) Н. і. висловлювань (а з відповідними змінами в кванторних правилах - до інтуїционістському Н. і. предикатів; см. математичний інтуїционізм , конструктивний напрям ).

Доведення в Н. і. - це, як правило, висновок з порожньої безлічі посилок. У формулюваннях Н. і., Подібних наведеній, в яких немає аксіом (окрім, можливо, А А), джерелом отримання «логічних законів», які висловлюються формулами, доказовими без залучення яких би то ні було гіпотез (посилок), виявляється правило É -введення. Гнучкість апарату Н. і., Близькість його до звичних форм змістовних міркувань і простота виходять висновків роблять його зручним знаряддям логіко-математичного дослідження. Н. і. корисно і в тих випадках, коли застосовуються інші системи логіки: в якості джерела виведених (додаткових) правил виведення, застосування яких також значно спрощує логічний апарат, а також для отримання евристичних (попередніх, які підлягають подальшому обґрунтуванню) доводів, які так чи інакше повинні передувати будь-якого формального доказу (як джерело доказуваних або спростовуваних гіпотез).

Літ .: Кліні С. К., Введення в метаматематику, пров. з англ., М., 1957, §§ 20, 23; Генцен Г., Дослідження логічних висновків, пров. с. нім., в кн .: Математична теорія логічного висновку, М., 1967; Каррі Х. Б., Підстави математичної логіки, пер. з англ., М., 1969. Див. також літ. при ст. правило виводу .

Ю. А. Гаст.