межа

Перед е л, одне з основних понять математики. П. - постійна, до якої необмежено наближається деяка змінна величина, що залежить від іншої змінної величини, при певному зміні останньої. Найпростішим є поняття П. числової послідовності, за допомогою якого можуть бути визначені поняття П. функції, П. послідовності точок простору, П. інтегральних сум.

Межа послідовності. Нехай задана послідовність дійсних чисел xn, n = 1, 2, ... Число а називається межею цієї послідовності, якщо для будь-якого числа e> 0 існує такий номер ne, що для всіх номерів n ³ ne виконується нерівність | xn - a | <E. В цьому випадку пишеться

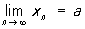
(Lim - перші букви латинського слова limes), або

xn ® a при n ® ¥.

Для П. послідовностей мають місце формули

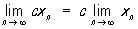(C - постійна)

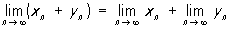
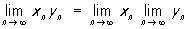
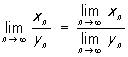
Ці формули справедливі в припущенні, що П., що стоять в їх правих частинах, існують, причому у формулі для П. приватного xn / yn треба ще додатково зажадати, щоб 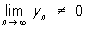. Якщо xn £ yn і послідовності xn і yn, n = 1, 2, ... сходяться, то

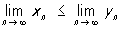
т. е. при граничних переходах несуворі нерівності зберігаються (але з xn <yn не випливає 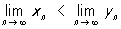, Наприклад, 1 / n> 0, n = 1, 2, ... проте 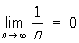). якщо 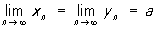і xn £ zn £ yn, то послідовність zn, n = 1,2, ..., сходиться до того ж П .:

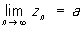
Послідовність an, n = 1, 2, ..., що сходиться до нуля, називається нескінченно малою. Послідовність сходиться до якого-небудь числа тоді і тільки тоді, коли різниця між членами послідовності і цим числом є нескінченно малою послідовністю (т. О., Загальне поняття П. послідовності зводиться до поняття нескінченно малої ). Так, наприклад, послідовність 1/2, 2/3, 3/4, ..., n / (n + 1), ... має своїм П. одиницю, оскільки різниця 1 - n / (n + 1) = 1 / (n + 1), n = 1, 2, ... є нескінченно малою послідовністю.

Будь-яка зростаюча (спадна) послідовність, обмежена зверху (відповідно знизу), сходиться. Наприклад, якщо для заданого числа а позначити через an наближене значення його кореня 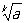(K - натуральне число) з n десятковими знаками після коми, обчислене з недоліком, то an £ an + 1 £ 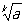, N = 1, 2, ..., тому послідовність an, сходиться, причому з нерівності 0 £ 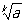- an £ 10-n випливає, що 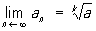. Др. прикладом зростаючої обмеженої зверху послідовності є послідовність довжин периметрів правильних багатокутників, вписаних в дану окружність, до довжини якої сходиться ця послідовність.

Для того щоб сходилася довільна послідовність xn, необхідно і достатньо, щоб вона задовольняла критерію Коші: для будь-якого числа e> 0 існує такий номер N e, що для всіх номерів m ³ N e і n ³ N e виконується нерівність | xn - xm | <E.

Якщо послідовність xn, n = 1, 2, ..., така, що для числа e> 0 існує такий номер ne, що для всіх номерів n ³ ne виконується нерівність | xn | > E, то послідовність xn, називається нескінченно великою і пишеться

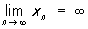
Якщо ж при цьому для будь-якого e> 0 існує такий номер ne, що xn> e (відповідно xn <- e) для всіх n ³ ne, то пишеться 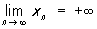(відповідно )

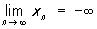Ці П. називаються нескінченними. наприклад, 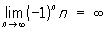. У разі ж послідовності n2, n = 1, 2, ... ,, можна написати не тільки 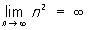але і більш точне рівність 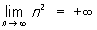. Само собою зрозуміло, що нескінченно великі послідовності не є сходяться в сенсі даного вище визначення цього поняття. На нескінченні П. переносяться далеко не всі властивості кінцевих П. Наприклад, послідовності xn = n і yn = 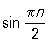- n нескінченно великі, а послідовність xn + yn ,, n = 1, 2, ..., обмежена і до того ж розходяться.

Часткові межі. Верхній і нижній межі. П. (кінцевий і нескінченний) будь-якої підпослідовності називається частковим межею останньої. З будь-якої обмеженої послідовності можна виділити сходящуюся підпослідовність (теорема Больцано - Вейерштрасса), а з будь-якої необмеженої - нескінченно велику. У безлічі всіх часткових П. послідовності завжди є як найбільший, так і найменший (кінцевий або нескінченний). Найбільший (відповідно найменший) частковий П. послідовності xn, n = 1, 2, ..., називають її верхнім (відповідно нижнім) межею і позначається 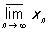(відповідно 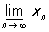). наприклад,

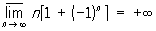
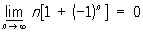
Послідовність має кінцевий або нескінченний П. тоді і тільки тоді, коли її верхній П. збігається з нижнім, при цьому їх загальне значення і є її П. Кінцевий верхній П. послідовності можна також визначити як таке число а, що при будь-якому e> 0 існує нескінченно багато членів послідовності, більших, ніж а - e, і лише трохи більше, ніж кінцеве число членів, більших, ніж a + e.

Межа функції. Нехай функція f, що приймає дійсні значення, визначена в деякому околі точки x0, крім, можливо, сам про і точки x0. Функція f має П. в точці x0, якщо для будь-якої послідовності точок xn, n = 1, 2, ..., xn ¹ x0, яка прагне до точки x0, послідовність значень функції f (xn) сходиться до одного і того ж числа А , яке і називається межею функції f в точці x0, (або при x ® x0) при цьому пишеться

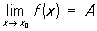
або

f (x) ® A при x ® x0

В силу цього визначення на П. функцій переносяться властивості П. суми, твори і приватного послідовностей, а також збереження нерівностей при граничному переході.

Визначення П. функції можна сформулювати і не вдаючись до поняття П. послідовності: число А називається границею функції f в точці x0, якщо для будь-якого числа e> 0 існує таке число d> 0, що для всіх точок х ¹ x0, які відповідають умові ½ х - x0 ½ <d, x ¹ x0, виконується нерівність ½ f (x) - A ½ <e.

Всі основні елементарні функції: постійні, статечна функція х a, показова функція ax, тригонометричні функції sin x, cos x, tg x і ctg x і зворотні тригонометричні функції arcsin x, arccos x, arctg x і arcctg x у всіх внутрішніх точках своїх областей визначення мають П., співпадаючі з їх значеннями в цих точках. Але це не завжди буває так. функція

,

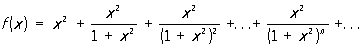що є сумою нескінченної геометричної прогресії зі знаменником q = 1 / (1 + x2), 0 <q <1, в точці х = 0 має П., рівний 1, бо f (x) = 1 + x2 при x ¹ 0. Цей П. не збігається зі значенням функції f в нулі: f (0) = 0. Функція ж

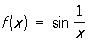, X ¹ 0,

зовсім не має П. при х ® 0, бо вже для значень xn = 1 / (p / 2 + p n) послідовність відповідних значень функції f (xn) = (- 1) n не має П.

Якщо П. функції при х ® х0 дорівнює нулю, то вона називається нескінченно малою при х ® х0. Наприклад, функція sin x нескінченно мала при х ® 0. Для того щоб функція f мала при х ® х0 П., рівний А, необхідно і достатньо, щоб f (x) = A + a (x), де a (х) є нескінченно малою при х ® х0

Якщо при визначенні П. функції f в точці x0 розглядаються тільки точки х, що лежать лівіше (правіше) точки x0, то виходить П. називається межею зліва (справа) і позначається 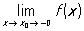(відповідно ).

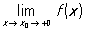Функція має П. в деякій точці, якщо її П. зліва в цій точці дорівнює її П. справа. Поняття П. функції узагальнюється і на випадок, коли аргумент прагне до нескінченності:

, ,

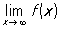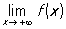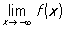
наприклад,

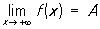
означає, що для будь-якого e> 0 існує таке d> 0, що для всіх х, що задовольняють умові x> d, виконується нерівність ½ f (x) - А ½ <e.

Прикладом функцій, завжди мають П., є монотонні функції . Так, якщо функція f визначена на інтервалі (а, b) і не убуває, то в кожній точці х, а <х <b, вона має кінцевий П. як зліва, так і справа; в точці в П. справа, який кінцевий тоді і тільки тоді, коли функція f обмежена знизу, а в точці b П. зліва, кінцевий в тому і тільки в тому випадку, коли функція обмежена зверху. У загальному ж випадку прагнення до П. може носити різний, необов'язково монотонний характер. Наприклад, функція f (x) = x 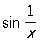при х ® 0 прагне до нуля, нескінченне число разів переходячи від зростання до спадаючій і назад.

Т. н. внутрішній критерій (критерій Коші) існування П. функції в точці полягає в наступному: функція f має в точці x0 П. в тому і тільки в тому випадку, якщо для будь-якого e> 0 існує таке d> 0, що для всіх точок х ' і х '', які відповідають умові ½ х '- x0 ½ <d, ½ x' '- x0 ½ <d, x' ¹ x0, x '' ¹ x0, виконується нерівність ½ f (x '') - f (x ') ½ <e.

Для функцій, як і для послідовностей, визначаються поняття безконечних П. вигляду 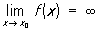, , 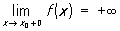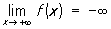і т.д.; в цих випадках функція f називається нескінченно великою при х ® х0, При х ® х0 + 0 або При х ® + ¥ відповідно і т.д. наприклад,

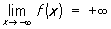
означає, що для будь-якого e> 0 існує таке d> 0, що для всіх х, що задовольняють умові х <- d, виконується нерівність f (x)> e.

Розширення поняття границі функції. Якщо функція f визначена на деякій множині Е числової прямої і точка x0 така, що в будь-який її околиці є точки безлічі Е, то аналогічно даному вище визначенню П. функції, заданої в деякій околиці точки x0, крім, можливо, самої точки x0, визначається поняття границі функції по безлічі Е

,

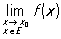для цього слід лише у визначенні П. завжди додатково вимагати, щоб точка х належала безлічі Е: х Î Е. П. послідовності xn, n = 1, 2, ..., є при такому визначенні поняття П. окремим випадком П. функції по безлічі, а саме функції f, визначеною на множині натуральних чисел n формулою f (n) = xn, n = 1, 2, ....

Функція, що дорівнює нулю при раціональних х і одиниці при ірраціональних, не має П. при х ® 0, проте по безлічі раціональних чисел вона при х ® 0 має П., рівний нулю. Поняття П. числової функції по безлічі переноситься і на функції багатьох змінних. В цьому випадку можна говорити, зокрема, про П. в даному напрямку, про П. по даній кривій, по даній поверхні і т.д. Крім того, для функцій багатьох змінних виникає поняття повторного межі, коли граничний перехід відбувається послідовно по разним змінним, наприклад 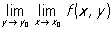. Поширюється поняття П. і на функції, які можуть приймати не тільки дійсні, а й комплексні значення.

Межа інтегральних сум. Ще одне важливе поняття П. виникає при визначенні інтеграла . Нехай, наприклад, функція f визначена на відрізку [a, b]. Сукупність {xi} таких точок xi, що

a = x0 <x1 <... <xi <... <xn-1 <xn = b,

наз. розбиттям відрізка [a, b]. Нехай x i-1 £ x I <xi, D xi = xi - xi-1, i = 1, 2, ..., n. Тоді сума f (x 1) D x1 + f (x 2) D x2 + ... + f (x n) D xn називається інтегральною сумою функції f. Число А є межею інтегральних сум і називається певним інтегралом:

,

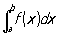якщо для будь-якого e> 0 існує таке d> 0, що яким би не було розбиття {xi} відрізка [a, b], для якого D xi <d, і які б не були точки xi, xi-1 £ x I £ xi, i = 1, 2, ..., n, виконується нерівність

½ f (x1) D x1 + f (x2) D x2 + ... + f (xn) D xn - A | <E.

Поняття П. інтегральних сум може бути введено і за допомогою П. послідовності.

Узагальнення поняття межі. З огляду на розмаїття вживаються в математиці спеціальних видів поняття П. природно виникло прагнення включити їх як окремий випадок в те або інше загальне поняття П. Наприклад, можна ввести поняття П., узагальнююче як поняття П. функції, так і поняття П. інтегральних сум. Система S непустих підмножин деякої множини Е називається напрямом, якщо для кожних двох підмножин А і В цієї системи виконується одне з включень А Ì В або B Ì A і перетин всіх множин з S порожньо. Нехай на безлічі Е задана числова функція f. Число а називається межею функції f у напрямку S, якщо для будь-якого e> 0 існує таке безліч А з S, що у всіх його точках виконується нерівність | f (x) - а | <E. При визначенні П. функції f в точці x0 за напрямок слід взяти сукупність всіх околиць цієї точки з досить малими радіусами за вирахуванням самої точки х 0. При визначенні П. інтегральних сум функції f, заданої на відрізку [а, b], слід розглянути безліч Е, елементами якого є всіляке розбиття відрізання [а, b] з вибраними в них точками x i. Підмножини E h безлічі Е, що відповідають розбиття, довжини D xi, відрізків яких не перевищують h, утворюють напрям. П. інтегральних сум (які, очевидно, є функціями, визначеними на безлічі Е) по вказаному напряму є інтеграл.

Поняття П. узагальнюється на ширші класи функцій, наприклад на функції, задані на частково впорядкованих множинах, або на функції, які є відображеннями одного простору (метричного або, більш загально, топологічного) на інше. Найбільш повно завдання визначення П. вирішується в топології і означає в загальному випадку, що деякий об'єкт, позначений f (x), який змінюється при змін ін. Об'єкта, позначеного через х, при досить близькому наближенні об'єкту х до об'єкту х 0 скільки завгодно близько наближається до об'єкта А. Основним в такого роду поняттях П. є поняття близькості об'єктів х і x 0, f (x) і А, які потребують математичного визначенні. Тільки після того як це буде зроблено, висловлену визначенням П. можна буде надати чіткий сенс і воно стане змістовним. Різні поняття близькості і вивчаються, зокрема, в топології.

Зустрічаються, однак, поняття П. ін. Природи, не пов'язані з топологією, наприклад поняття П. послідовності множин. Послідовність множин An, n = 1, 2, ..., називається збіжної, якщо існує така безліч А, зване її межею, що кожна його точка належить всім множинам A n, починаючи з деякого номера, і кожна точка з об'єднання всіх множин A n, яка не належить A, належить лише кінцевому числу A n.

Історична довідка. До поняття П. впритул підійшли ще давньогрецькі вчені при обчисленні площ і обсягів деяких фігур і тіл за допомогою вичерпання методу . так, Архімед , Розглядаючи послідовності вписаних і описаних ступінчастих фігур і тіл, за допомогою методу вичерпання доводив, що різниця між їх площами (відповідно об'ємами) може бути зроблена менше будь-який наперед заданої позитивної величини. Включаючи в себе уявлення про нескінченно малих, метод вичерпання був зародком теорії П. Однак в явному вигляді в давньогрецькій математиці поняття П. не було сформульоване, не було створено і будь-яких основ загальної теорії.

Новий етап в розвитку поняття П. настав в епоху створення диференціального й інтегрального числення. Г. Галілей , І. Кеплер , Б. Кавальєрі , Б. Паскаль і ін. широко використовують при обчисленні площ і обсягів «Неподільних» метод , Метод актуальних нескінченно малих, т. Е. Таких нескінченно малих, які, за їх уявленням, є незмінними величинами, які не дорівнюють нулю і разом з тим меншими по абсолютній величині будь-яких позитивних кінцевих величин. Продовжує в цей період застосовуватися і розвиватися і метод вичерпання ( Григорій з Сен-Вінцента, П. Гульдін , Х. Гюйгенс та ін.). На основі інтуїтивного поняття П. з'являються спроби створити загальну теорію П. Так, І. ньютон перший відділ першої книги ( «Про рух тіл») своєї праці «Математичні початки натуральної філософії» присвячує своєрідній теорії П. під назвою «Метод перших і останніх відносин», яку він бере за основу свого флюксий обчислення . У цій теорії Ньютон замість актуальних нескінченно малих пропонує концепцію «потенційною» нескінченно малої, яка лише в процесі свого зміни стає по абсолютній величині менше будь-який покладе, кінцевої величини. Точка зору Ньютона була істотним кроком вперед у розвитку уявлення про П. Поняття П., що намічалося в математиків 17 ст., В 18 ст. поступово все більше аналізувалося (Л. Ейлер , Ж. Д'Аламбер , Л. Карно , брати Бернуллі і ін.) і уточнювалося. У цей період воно служило лише для спроб пояснити правильність диференціального й інтегрального числення і ще не було методом розробки проблем математичного аналізу.

Сучасна теорія П. почала формуватися на початку 19 ст. в зв'язку з вивченням властивостей різних класів функцій, перш за все безперервних, а також у зв'язку зі спробою докази існування ряду основних об'єктів математичного аналізу (інтегралів функцій дійсних і комплексних змінних, сум рядів, алгебраїчних коренів і більш загальних рівнянь і т.п.). Вперше в роботах О. Коші поняття П. стало основою побудови математичного аналізу. Їм були отримані основні ознаки існування П. послідовностей, основні теореми про П. і. що дуже важливо, дан внутрішній критерій збіжності послідовності, що носить тепер його ім'я. Нарешті, він визначив інтеграл як П. інтегральних сум і вивчив його властивості, виходячи з цього визначення. Остаточно поняття П. послідовності і функції оформилося на базі теорії дійсного числа в роботах Б. Больцано і К. Вейєрштрасса . З подальших узагальнень поняття П. слід зазначити поняття П., дані в роботах С. О. Шатуновського (Опубліковано в 1923), американських математиків Е. Г. Мура і Г. Л. Сміта (1922) і французького математика А. Картана (1937).

Літ .: Александров П. С., Введення в загальну теорію множин і функцій, М. - Л., 1948; Ільїн В. А., Позняк Е. Р., Основи математичного аналізу, 3 вид., Т. 1-2, М., 1971-73; Кудрявцев Л. Д., Математичний аналіз, 2 видавництва., Т. 1-2, М., 1970; Нікольський С. М., Курс математичного аналізу, т. 1-2, М., 1973; Смирнов В. І., Курс вищої математики, 22 вид., Т. 1, М., 1967.

Л. Д. Кудрявцев.